The Universe
Cosmology is one of the most awe inspiring fields in all of science. To think that humans, a specie that originated $\sim 10^5$ years ago in Africa, standing on a speck of dust (the Earth), are able to understand the universe as a whole, it’s origin and evolution is indeed amazing. Here I decided to focus on two very interesting quantities, mentioned in the title, that are related to our universe and find their values based on the most recent observations and the standard cosmological model. The cosmological principle states that the universe is both homogeneous and isotropic on “large scales”, an assumption that is very well verified in observations such as the CMB being highly homogeneous (1 part in 100,000). This assumption significantly reduces the allowed metrics which describe the geometry of the universe, called the FRW metric:
\[ds^2=-c^2dt^2+a^2(t)[\frac{dr^2}{1-kr^2}+r^2(d\theta^2+\sin^2\theta d\phi^2)]\]Where $k$ is related to the curvature and can take the values $-1,0,1$ corresponding to a hyperbolic, Euclidean and spherical universes. The spatial part of the metric describes the geometry of a homogeneous and isotropic universe at a given time slice t. $a(t)$ is the scale factor which allows a temporal evolution of the spatial part of the metric. Specifically the spatial coordinates are co-moving and independent of any time evolution. The dynamics of the metric $g_{\mu \nu}$ is determined by Einstein’s field equations:
\[G_{\mu \nu}+g_{\mu \nu}\Lambda=\frac{8\pi G}{c^4}T_{\mu \nu}\]Focusing on the $00$ component we can get the following equation by plugging the FRW metric:
\[\frac{\dot a^2}{a^2}=\frac{8\pi G \rho}{3}-\frac{kc^2}{a^2}+\frac{\Lambda c^2}{3}\]We define the Hubble parameter: $H=\frac{\dot a}{a}$, which measures the expansion rate of the universe. In order to relate to the way observable quantities are reported we bring the equation into a convenient form by the following definitions. $\rho_c\equiv \frac{8\pi G\rho}{3H^2}$ which is called the critical density, since when $\rho=\rho_c$, we have $k=0$. And $\Omega_x\equiv\frac{\rho_x}{\rho_c}=\frac{8\pi G\rho}{3H^2}$ which measure the fraction of the energy density in a given component $x$ relative to the critical density. The density appearing in the equation can be separated to energy density due to radiation and due to matter $\rho=\rho_r+\rho_m$. The different components making up the energy density of the universe evolve differently with the evolution of the universe. Their evolution is determined from the conservation equation for the stress-energy tensor for each component \(T^{\mu}_{\nu;\mu}\), where $T^{\mu}_{\nu}=diag(\rho,-P,-P,-P)$. Plugging this into the energy conservation equation, we get for the evolution of the energy density:
\[\dot \rho=-3H(\rho+\frac{p}{c^2})\]The implication of this equation is that the expansion is adiabatic $dU=-pdV$ , $dS=0$. Considering now the different components, we have for ordinary matter (non-relativistic) $p=0$(since the energy density is dominated by the mass $p«\rho c^2$), plugging this to the equation gives $\rho\propto a^{-3}$. For radiation (or highly relativistic particles) we have $p=\frac{1}{3}\rho c^2$, plugging this into the equation gives $\rho \propto a^{-4}$. Finally for dark energy: $P=-\rho$, for which $\rho \propto const$.
Combining all of this we rewrite the equation in terms of the current time ($a=1$) $\Omega_0$ values:
\[\frac{H^2}{H_0^2}=\Omega_{r}a^{-4}+\Omega_ma^{-3}+\Omega_ka^{-2}+\Omega_{\Lambda}\]We see that since we define the quantities relative to the current values we have by plugging $a=1: \Omega_k+\Omega=1$, where $\Omega$ is the sum of all other components other than the curvature component.
The age of the universe is the time span in which the universe evolved from $a = 0$ to $a = 1$, therefor from the equation we can write using the definition of $H$:
\[t_0 = \frac{1}{H_0} \int_0^1 \frac{da}{a(\Omega_{r}a^{-4}+\Omega_m a^{-3}+\Omega_k a^{-2}+\Omega_{\Lambda})^{1/2}}\]I now list the most recent measurements at the time of writing (best fit values) of the above parameters obtained from the Planck satellite measuring the CMB [arXiv].
\[H_0 = 67.3 km/s/Mpc, \\ \Omega_m = 0.315, \\ \Omega_{r} = 10^{-4}, \\ \Omega_{\Lambda} = 0.685, \\ \Omega_{k} = -10^{-4}\]Plugging these values in the integral and calculating it numerically we get for the age of the universe:
\[t_0=13.81 \ {\rm Gyr}.\](With the last digit having some error associated with the measurement errors in the parameters).
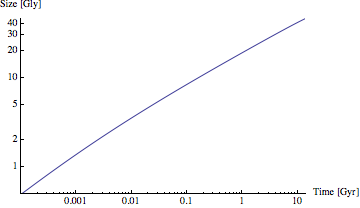
Next we estimate the size of the observable universe. Where observable means that light had enough time to reach our detectors. Since the universe is constantly expanding, the naive answer $R=ct_0$ is incorrect. The correct answer considers the path of photon in the FRW metric. Since for a photon we have $ ds^2=0$, and taking a radial trajectory in a flat space $(k=0)$ we get from (1):
\[R=\int \frac{cdt}{a}\]Rewriting this in terms of a and $H=\frac{\dot a}{a}$, which I have expressions for in terms of known quantities. we make the change
\[dt=\frac{da}{\dot a}=\frac{da}{a H}.\]Plugging this in (6):
\[R=\int_0^1 \frac{c da}{a^2 H(a)}=\int_0^1 \frac{c da}{a^2 H_0(\Omega_{r}a^{-4}+\Omega_m a^{-3}+\Omega_k a^{-2}+\Omega_{\Lambda})^{1/2}}\]Numerically calculating this integral gives for the radius of the observable universe:
\[R=46.2 Gly\]Below I show the size of the observable universe as a function of time.