Fake coins and infectious diseases
How to speed up detection and testing using pooling

Fake coins
Imagine there are 1000 coins out of which 1% are fake, where a fake coin can weigh a little less or more than a real coin. What is the fastest way to identify those 10 fake coins.
The slowest way would be to weigh each coin one-by-one, which will require 1000 weighings. Can we do better? Yes.
A better idea is known as pooling. Since we know only a small fraction of coins are fake, if we combine multiple coins into pools, some of these pools will contain only real coins allowing us to discard them, and remain with less coins to weigh.
The idea goes back to a paper by Robert Dorfman published in 1943, where this method was applied to Syphilis antibody detection in blood tests, where multiple blood samples were pooled together and tested together.
Returning to the toy example of the coins, we divide the coins into pools of coins, and weigh each pool separately. Since we know the expected weight of a pool of real coins, we would know which pools contain fake coins, however we don’t which are the individual fake coins yet.
What is the advantage of pooling?
The probability of any coin being fake is $r=0.01$ (the prevalence of fakes in the available coins). Therefore, the probability of a pool of $s_1$ coins having at least one fake coin is:
\[p_1 = 1 - (1-r)^{s_1}.\]This is the complementary probability of all the coins being real, $(1-r)^{s_1}$.
If we divide the $N=1000$ coins into $N/s_1$ pools and weigh each pool, the expected number of pools that contain at least one fake coin is, $p_1\frac{N}{s_1}$. The power of the pooling technique is that $(1-p_1)\frac{N}{s_1}$ pools, will have all real coins, and therefore can be discarded. The coins in the remainig suspicious pools can then be weighed individually. What is the total number of weighings we need to do?
\[T = N\left(\frac{1}{s_1} + p_1\right)\]As an example, if we choose $s_1=20$, we have 50 initial pools of coins, out of which 41 pools will be discarded, and the expected number of weighings to be able to identify all fake coins is, $145$, a factor of ~7 improvement. We see that the number of weighings or tests as a fraction of $N$ is independent of $N$.
How to choose the optimal pool size?
To get the optimal pool size, which will give the least amount of weighings, we need to minimize the expression for the number of tests $T$, by varying $s_1$.
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
from numpy.random import choice
import scipy.optimize as optimize
from typing import List, Tuple
import seaborn as sns
def tests(pools: List[float], r: float) -> float:
"""
Calculate expected value of tests, as percentage of population
"""
def p_frac(s: int, r: float) -> float:
"""
helper function to Calculate p
from prevelance r and pool size s
"""
return 1 - (1 - r)**s
r_val = r/100.0
total_tests = 0
r_vals = [r_val]
p_vals = [1]
s_vals = []
for i in range(len(pools)):
s_vals.append((pools[i]))
p_vals.append(p_frac(s_vals[i], r_vals[i]))
r_vals.append(r_vals[i]/p_vals[i+1])
total_tests += 1/s_vals[i]*np.prod(p_vals[:-1])
total_tests += np.prod(p_vals)
return total_tests*100
def optim(n_pools: int, r: float) -> Tuple:
"""
Find optimal pool sizes for given number of poolings
and prevalence r.
parameters:
- n_pools: number of pools
- r: prevalence (percentage)
returns:
list of pool sizes and expected number of tests as
percentage of population
"""
initial_pools = [5*(i+1) for i in range(n_pools)]
initial_pools.reverse()
bounds = [(1,5000)]*n_pools
res = optimize.minimize(tests,
initial_pools,
bounds=bounds,
method='L-BFGS-B',
options={'maxiter':5e7},
args=(r),
tol=1e-15)
s=[]
for v in res.x:
s.append(v)
T = tests(s, r)
return s, T
Using the above optimization method for prevalence of $1\%$ gives:
N=1000
print(f"Optimal pool size: {int(np.floor(optim(n_pools=1, r=1)[0][0]))}")
print(f"Number of weighings: {int(np.ceil(optim(n_pools=1, r=1)[1]*N/100))}")
Optimal pool size: 10
Number of weighings: 196
A significant improvement over the original $1000$ weighings.
A natural extension is to continue the pooling, known as nested-pooling, i.e. we divide the pools following the first weighing to new pools, with a different pool size, which can again be determined by minimizing the expression for the number of test, in this case of 2-pools given by a slightly more complex expression:
\[T = N\left(\frac{1}{s_1} + \frac{p_1}{s_2} + p_1p_2\right)\]where $s_1, s_2$ are the first and second pool sizes, respectively. $p_1$ is as before, and $p_2 = 1 - (1-\frac{r}{p_1})^{s_2}$ is the modified probability for the second batch of pools.
I’ve been using the word “expected” number of weighings because we are dealing with probabilities and randomness in the separation of the coins into pools, therefore we are dealing with a distribution of possible values, the expected value of which is given by the formulas above. To demonstrate this we can actually run simulations of the pooling and record the number of required weighings.
def run_tests(S1:int = 9, S2:int = None, r:float = 1, N:int = 10**6) -> float:
"""
Run pooling and testing simulation (up to 2 pools)
retuns number of tests as fraction of population
parameters:
N - populationsize
S - pool size
r - prevalence (%)
returns:
tests as precentage of population
"""
pop = np.arange(1,N+1)
infected = set(choice(pop, int(r/100.*N), replace=False))
n_buckets = int(np.ceil(N/S1))
pop_perm = np.random.permutation(pop)
buckets = np.array_split(pop_perm, n_buckets)
positive_pop = []
for bucket in buckets:
if not infected.isdisjoint(bucket):
positive_pop.extend(bucket)
if S2:
# second pool
n_buckets2 = int(np.ceil(len(positive_pop)/S2))
positive_pop_perm = np.random.permutation(positive_pop)
buckets2 = np.array_split(positive_pop_perm, n_buckets2)
positive_pop2 = set()
for bucket in buckets2:
if not infected.isdisjoint(bucket):
positive_pop2.update(bucket)
total_tests = len(buckets) + len(buckets2) + len(positive_pop2)
else:
# Total number of test to get individual results
total_tests = n_buckets + len(positive_pop)
# fraction of population tested
pop_frac = (total_tests)*100/N
return pop_frac
Running the tests multiple times for our example of the coins gives.
N=1000
a=[]
for i in range(5000):
a.append(run_tests(S1=10, r=1, N=1000))
print(f"Weighings = {N*np.mean(a)/100:.0f} +- {N/100*np.std(a):.0f}")
Weighings = 196 +- 6
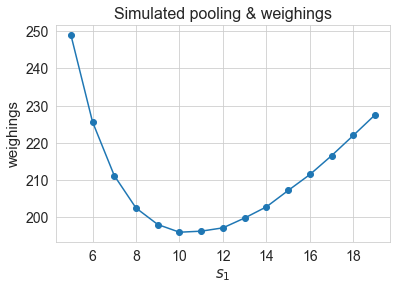
We can also simulate for different pool sizes and check if the above choice is indeed optimal.
s=np.arange(5,20)
means = []
for s1 in s:
a=[]
for i in range(1000):
a.append(run_tests(S1=s1, r=1, N=1000))
means.append(np.mean(a)*N/100)
plt.plot(s,means,marker='o');
plt.xlabel(r'$s_1$', fontsize=15);
plt.ylabel('weighings', fontsize=15);
plt.xticks(fontsize=14);
plt.yticks(fontsize=14);
plt.title("Simulated pooling & weighings", fontsize=16);
What about 2-pools? The above optimization method gives:
N=1000
pools = np.floor(optim(n_pools=2, r=1)[0]).astype(int)
weighings = int(np.ceil(optim(n_pools=2, r=1)[1]*N/100))
print(f"Optimal pools size: {pools}")
print(f"Total number of weighings: {weighings}")
Optimal pools size: [24 5]
Total number of weighings: 131
A further reduction of 65 weighings.
Note that pooling is most efficient when the prevelance is low, allowing to discard larger number of pools.
Infectious disease
This idea of pooling can be generalized to the case of detecting infected individuals in a susceptible population for an infectious disease. The crucial difference is the “weighing” method, which in the case of detecting infected individuals, is the qPCR method, which is highly accurate way to identify the presence of a target DNA/RNA in a pooled sampled of DNAs.
My friend Yossi Eliaz (@YossiEliaz) and I have explored this in a paper we published in medRxiv recently, demonstrating the great benefits of the pooling technique for testing for SARS-CoV-2 in a population with an estimated prevalance obtained from a SIRD model fit to reported infections and deaths.